2-distribution (k2) Gaussian Mixture Model — normal_k2

Estimates the parameters of a 2 distribution mixture model via expectation maximization.

S3 plot method for "mix_k2" objects.

Usage

normal_k2_mixture(
  data,
  pars = list(start_mu = NULL, start_sd = NULL, start_pi = NULL),
  max_iter = 1000,
  max_restarts = 25,
  eps = 1e-08
)

# S3 method for class 'mix_k2'
plot(x, type = c("density", "likelihood", "posterior"), title = NULL, ...)

Arguments

data: numeric(n).
pars: Initial values for start_mu, start_sd, and start_pi.
max_iter: integer(1). Max number of iterations to perform.
max_restarts: integer(1). Max number of restarts ro perform.
eps: double(1). Machine precision for when to stop the algorithm.
x: A mix_k2 object generated from normal_k2_mixture.
type: character(1). Matched string one of: "density", "likelihood" or "posterior".
title: character(1). Title for the plot.
...: Additional parameters for extensibility.

Value

A mix_k2 class object.

References

Tibshirani and Hastie

See Tibshirani and Hastie ("bible"); pg. 273.

Author

Stu Field

Examples

# Generate 2 gaussian distributions
x <- withr::with_seed(101,
  c(rnorm(100, mean = 10, sd = 1), rnorm(100, mean = 2, sd = 2)))
mix_theta <- normal_k2_mixture(x)
#> ✓ Iteration ... 18
mix_theta
#> ══ Mix Type: normal_k2_mixture ═══════════════════════════════════════════
#> • n               200
#> • iter            18
#> • mu              [9.97, 1.941]
#> • sigma           [0.924, 2.033]
#> • pi_hat          0.502
#> • lambda          [0.498, 0.502]
#> • final loglik    -483.915
#> ══════════════════════════════════════════════════════════════════════════

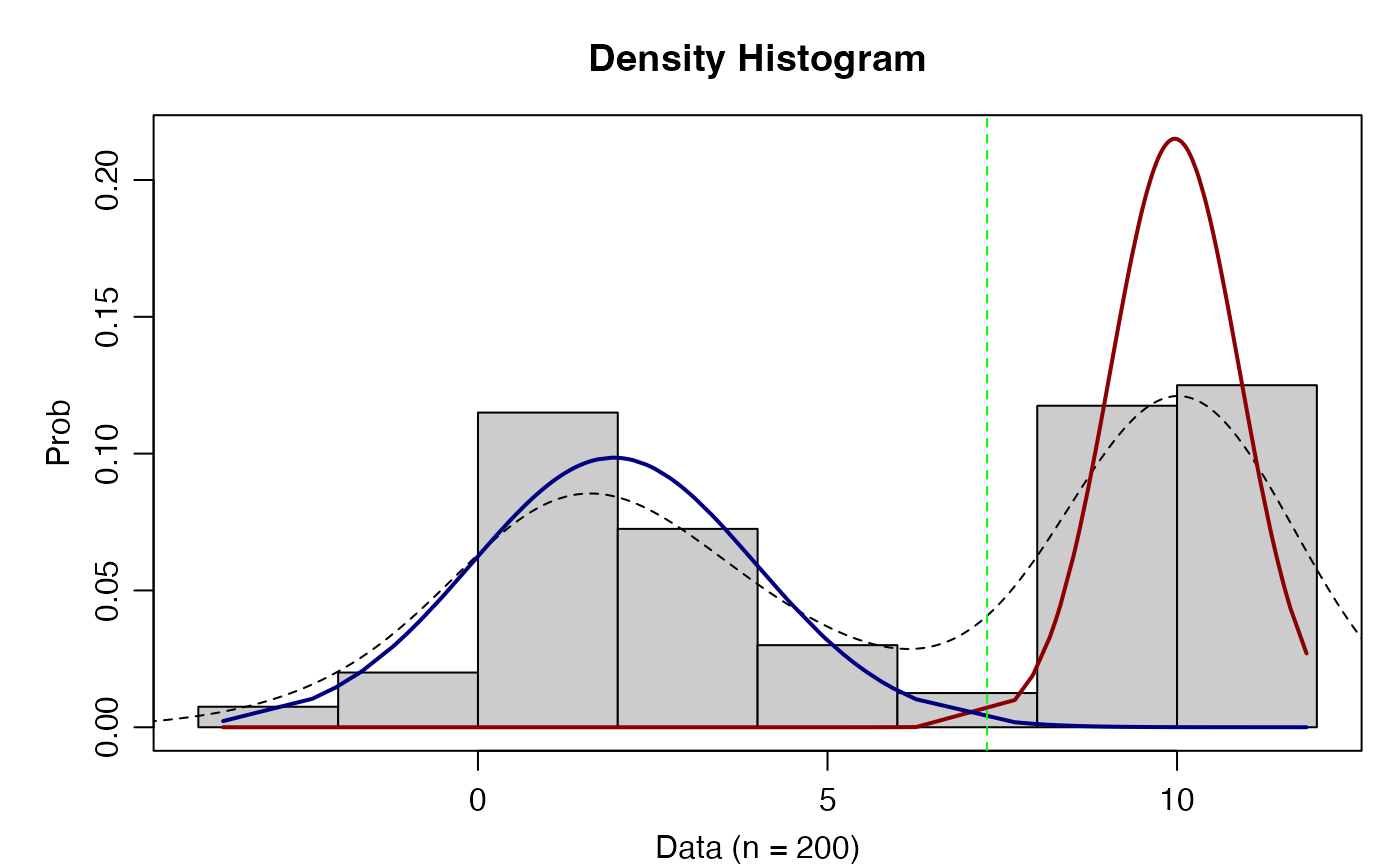
plot(mix_theta)

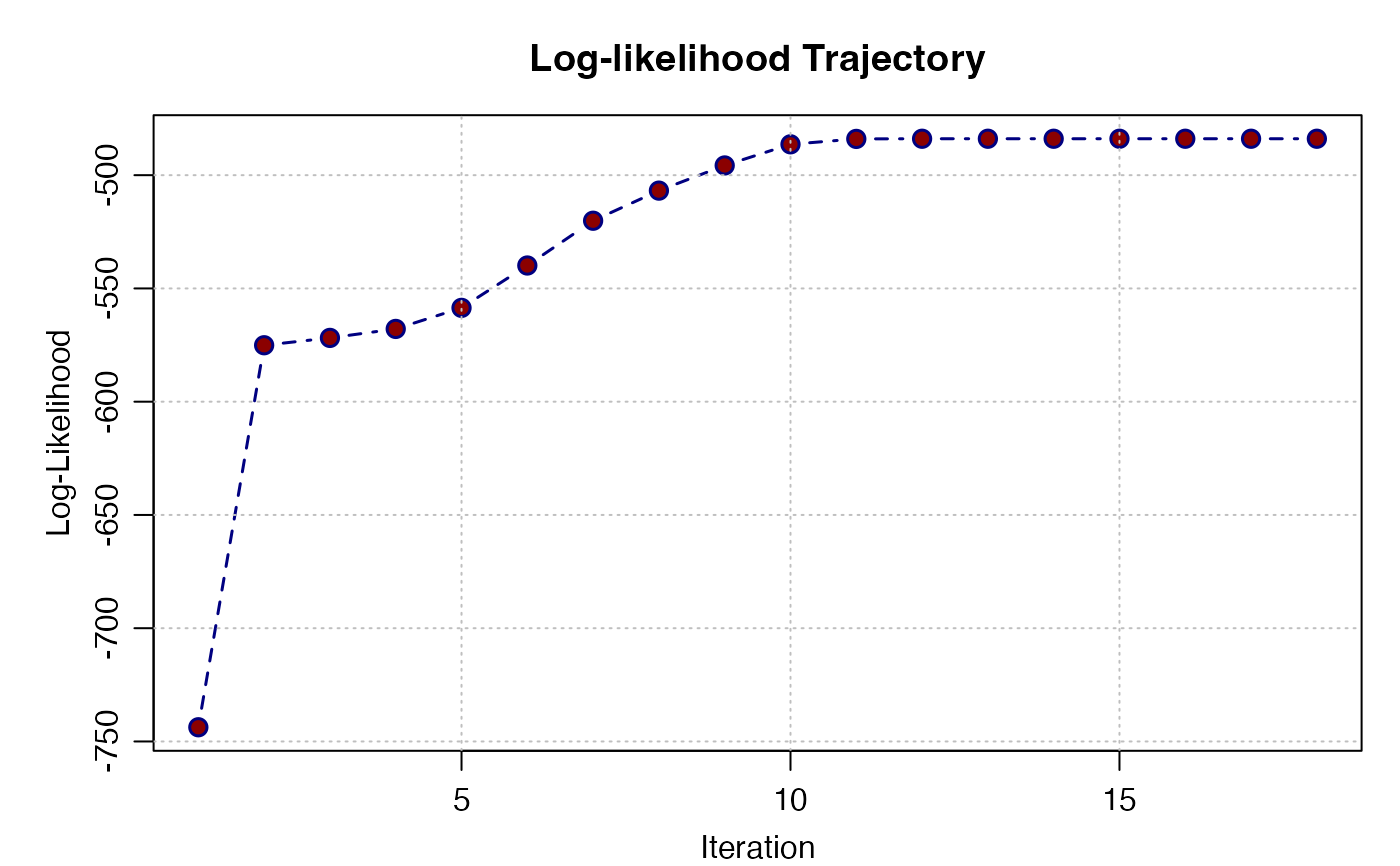
plot(mix_theta, "like")

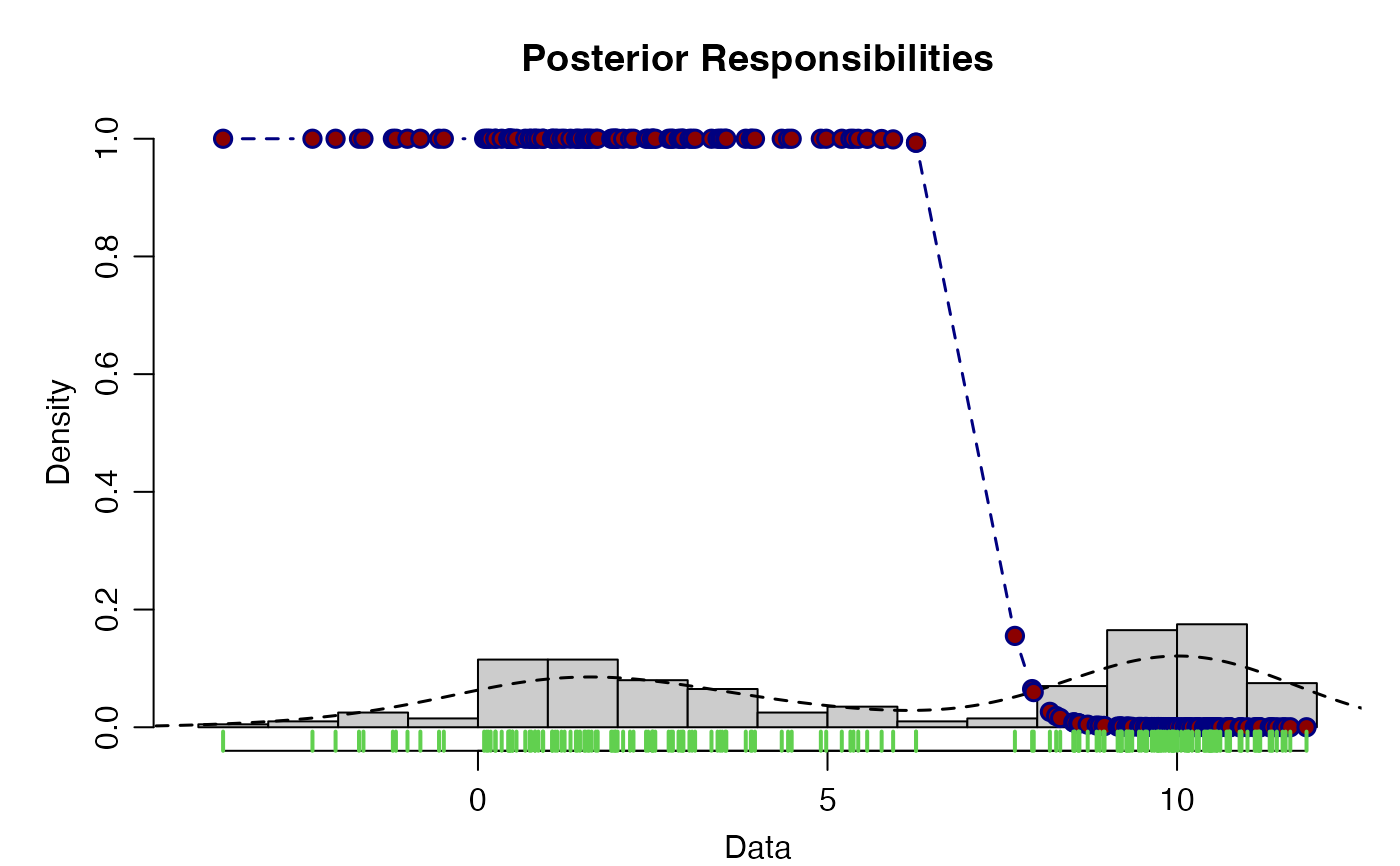
plot(mix_theta, "post")